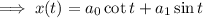Mathematics, 02.11.2019 04:31 andrejr0330jr
Assume a series solution x(t) =summation ^ infinity _ n = 0 a_n t ^n for the equation x" + x = 0. show that the recursion formula for the coefficients is a_m + 2= -a _m/(m + l1(m + 2), m = 0, 1, and that this leads to the general solution x (t) = a_0 (1 - t^2/2! + t^4/4! + +a_1 (t - t^3/3! + t^5/5! + = a_0 cos(t) + a_1 sin(t)

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 20:30
Aregular pan has a length that is 4/3 the width. the total area of the pan is 432in.2. what is the width of the cake pan?
Answers: 1

Mathematics, 22.06.2019 00:00
The letters g e o r g i a are placed in a bag . if you picked a card and knew it was a vowel , what is the probability that it is an a ?
Answers: 1


Mathematics, 22.06.2019 02:20
According to the general equation for conditional probability, if p(ab) = 4/5 and p(b)= 5/6, what is p(a|b)? a. 8/9 b. 35/36 c. 24/25 d. 15/16
Answers: 2
You know the right answer?
Assume a series solution x(t) =summation ^ infinity _ n = 0 a_n t ^n for the equation x" + x = 0. sh...
Questions


Business, 07.01.2021 18:40


Chemistry, 07.01.2021 18:40

Mathematics, 07.01.2021 18:40


Health, 07.01.2021 18:40

Mathematics, 07.01.2021 18:40

Biology, 07.01.2021 18:40



Mathematics, 07.01.2021 18:40


Biology, 07.01.2021 18:40



English, 07.01.2021 18:40





![\displaystyle\sum_{n\ge0}\bigg[(n+1)(n+2)a_{n+2}+a_n\bigg]t^n=0](/tpl/images/0356/4460/cf923.png)

 , given
, given  and
and  . Now,
. Now,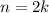 for integer
for integer  , then
, then




 , then
, then