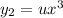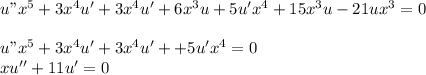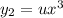Mathematics, 08.01.2020 04:31 ugum
We know that y1(x)=x3 is a solution to the differential equation x2d2y+5xdy−21y=0 forx∈(0,[infinity]).
use the method of reduction of order to find a second solution tox2d2y+5xdy−21y=0 for x∈(0,) after you reduce the second order equation by making the substitution w=u′, you get a first order equation of the form w′=f(x, w)=(b) y2(x)=?

Answers: 2


Another question on Mathematics

Mathematics, 21.06.2019 12:30
Country carpets charges $22 per square yard for carpeting, and an additional installation fee of $100. city carpets charges $25 per square yard for the same carpeting, and an additional installation fee of $70
Answers: 2

Mathematics, 21.06.2019 15:20
Can (3,5 and square root 34) be sides on a right triangle?
Answers: 1

Mathematics, 21.06.2019 15:30
Write an equation of a line in slope intercept form that is perpendicular to the line 2x -3y = 12 and passes through the point (2, 6).
Answers: 3

Mathematics, 21.06.2019 15:50
3-12. write each answer with a reasonable number of figures. find the absolute uncertainty and percent relative uncertainty for each answer. (a) [12.41 (±0.09) + 4.16 (±0.01)] x 7.068 2 (±0.000 4) =? (b) [3.26 (±0.10) x 8.47 (±0.05)] - 0.18 (±0.06) =? (c) 6.843 (±0.008) x 104 + [2.09 (±0.04)- 1.63 (±0.01)] =?
Answers: 1
You know the right answer?
We know that y1(x)=x3 is a solution to the differential equation x2d2y+5xdy−21y=0 forx∈(0,[infinity]...
Questions



Spanish, 21.07.2019 16:00



Spanish, 21.07.2019 16:00

English, 21.07.2019 16:00






German, 21.07.2019 16:00


Mathematics, 21.07.2019 16:00





Mathematics, 21.07.2019 16:00

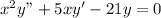 ,where x can take any positive value
,where x can take any positive value