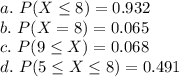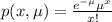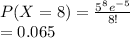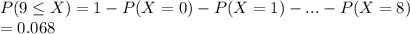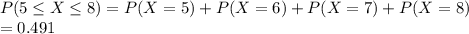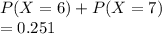Let X, the number of flaws on the surface of a randomly selected boiler of a certain type, have a Poisson distribution with parameter μ = 5. Use the cumulative Poisson probabilities from the Appendix Tables to compute the following probabilities. (Round your answers to three decimal places.)

(a) P(X ≤ 8)
(b) P(X = 8)
(c) P(9 ≤ X)
(d) P(5 ≤ X ≤ 8)
(e) P(5 < X < 8)

Which expression calculates the speed in meters per second of an object that travels a distance of 100 m every 20 seconds

It says factor each expression 49x-28?

Does the function satisfy the hypotheses of the mean value theorem on the given interval? f(x) = 4x^2 + 3x + 4, [−1, 1] no, f is continuous on [−1, 1] but not differentiable on (−1, 1). no, f is not continuous on [−1, 1]. yes, f is continuous on [−1, 1] and differentiable on (−1, 1) since polynomials are continuous and differentiable on . there is not enough information to verify if this function satisfies the mean value theorem. yes, it does not matter if f is continuous or differentiable; every function satisfies the mean value theorem.