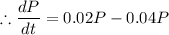Determine a differential equation that models the growth of a population of fish as a function of time in days under each of the following hypotheses: a) The rate of population increase is proportional to the size of the population. The population increases by 2 percent per day. (Treat time in days as a continuous variable, i. e. the rate at which the population increases is .02 times the population size.) dP/dt =
b) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 4 percent of the population is harvested each day. dP/dt =
c) The rate of population increase is again proportional to the size of the population with the same constant of proportionality but 1000 fish are harvested each day. dP/dt =
d) The equation in part c) has a threshhold. What is it?