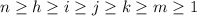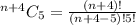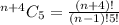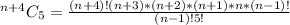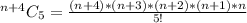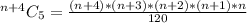Mathematics, 12.03.2021 15:30 kirkhester1
If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which the elements of the 5-tuple are written in increasing order but are not necessarily distinct? In other words, how many 5-tuples of integers (h, i, j, k, m) are there with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n? As in Example 9.6.3, you can represent any ordered 5-tuple of integers (h, i, j, k, m) with 1 ≤ h ≤ i ≤ j ≤ k ≤ m ≤ n as a string of n − 1 vertical bars and 5 crosses, with the position of crosses indicating which 5 integers from 1 to n are included in the 5-tuple. Thus, the number of 5-tuples is the same as the number of strings of n+4 vertical bars and 5 crosses, which is n(n+1)(n+2)(n+3)(n+4) 120 .

Answers: 3


Another question on Mathematics

Mathematics, 21.06.2019 18:30
What can each term of the equation be multiplied by to eliminate the fractions before solving? x – + 2x = + x 2 6 10 12
Answers: 1

Mathematics, 21.06.2019 19:30
If you can solve all of these i will give ! - 4% of 190 - 4% of 162.5 - 4% of 140 - a 4% increase from 155.1 - a 4% increase from 159.8
Answers: 2


Mathematics, 21.06.2019 23:00
Is a square always, sometimes, or never a parallelogram
Answers: 2
You know the right answer?
If n is a positive integer, how many 5-tuples of integers from 1 through n can be formed in which th...
Questions


Mathematics, 16.08.2019 08:30

Mathematics, 16.08.2019 08:30


Mathematics, 16.08.2019 08:30

History, 16.08.2019 08:30

History, 16.08.2019 08:30

Physics, 16.08.2019 08:30





Mathematics, 16.08.2019 08:30




Mathematics, 16.08.2019 08:30



History, 16.08.2019 08:30

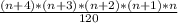
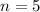
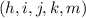 implies that:
implies that:
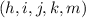 are there such that
are there such that