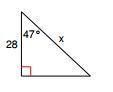
Mathematics, 26.08.2021 18:40 HHHHHHHHHMMMMMMMMM
Verify that y = tan(x + c) is a one-parameter family of solutions of the differential equation y' = 1 + y2. Differentiating y = tan(x + c) we get y' = 1 + sec2(x + c) or y' = 1 + y2. Differentiating y = tan(x + c) we get y' = 1 + tan2(x + c) or y' = 1 + y2. Differentiating y = tan(x + c) we get y' = csc(x + c) or y' = 1 + y2. Differentiating y = tan(x + c) we get y' = sec(x + c) or y' = 1 + y2. Differentiating y = tan(x + c) we get y' = tan2(x + c) or y' = 1 + y2. (b) Since f(x, y) = 1 + y2 and ∂f/∂y = 2y are continuous everywhere, the region R in Theorem 1.2.1 can be taken to be the entire xy-plane. Use the family of solutions in part (a) to find an explicit solution of the first-order initial-value problem y' = 1 + y2, y(0) = 0.

Answers: 2


Another question on Mathematics



Mathematics, 21.06.2019 22:10
If p(a) = 0.70 and p(b) = 0.20, then a and b are independent events if
Answers: 3

You know the right answer?
Verify that y = tan(x + c) is a one-parameter family of solutions of the differential equation y' =...
Questions

Chemistry, 22.04.2021 01:00


Mathematics, 22.04.2021 01:00


Mathematics, 22.04.2021 01:00


Mathematics, 22.04.2021 01:00





Arts, 22.04.2021 01:00






Mathematics, 22.04.2021 01:00

Mathematics, 22.04.2021 01:00