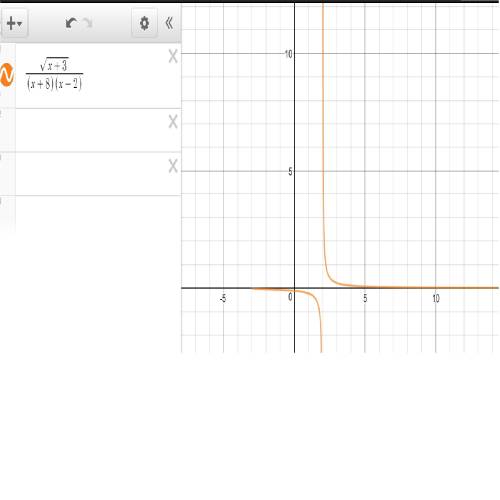
1. find the domain of the given function. (1 point)
f(x) = square root of quantity x plus three divided by quantity x plus eight times quantity x minus two.
a) x > 0
b) all real numbers
c) x ≥ -3, x ≠ 2
d) x ≠ -8, x ≠ -3, x ≠ 2
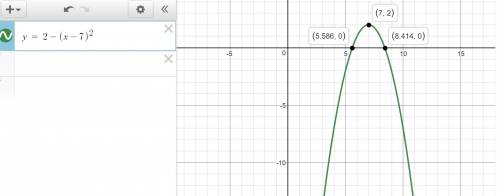
2. identify intervals on which the function is increasing, decreasing, or constant.
g(x) = 2 - (x - 7)2 (1 point)
a) increasing: x < 2; decreasing: x > 2
b) increasing: x < -7; decreasing: x > -7
c) increasing: x < 7; decreasing: x > 7
d)increasing: x > 2; decreasing: x < 2
3. perform the requested operation or operations.
f(x) = 4x + 7, g(x) = 3x2
find (f + g)(x). (1 point)
a) four x plus seven divided by three x squared.
b) 12x3 + 21x
c) 4x + 7 + 3x2
d) 4x + 7 - 3x2
4. perform the requested operation or operations.
f(x) = x minus five divided by eight. ; g(x) = 8x + 5, find g(f( (1 point)
a) g(f(x)) = x - five divided by eight.
b) g(f(x)) = x
c) g(f(x)) = 8x + 35
d) g(f(x)) = x + 10
5. find f(x) and g(x) so that the function can be described as y = f(g(
y = nine divided by square root of quantity five x plus five. (1 point)
a) f(x) = nine divided by square root of x. , g(x) = 5x + 5
b) f(x) = square root of quantity five x plus five. , g(x) = 9
c) f(x) = nine divided by x. , g(x) = 5x + 5
d) f(x) = 9, g(x) = square root of quantity x plus five
6. a satellite camera takes a rectangular-shaped picture. the smallest region that can be photographed is a 4-km by 4-km rectangle. as the camera zooms out, the length l and width w of the rectangle increase at a rate of 3 km/sec. how long does it take for the area a to be at least 4 times its original size? (1 point)
a) 4.94 sec
b) 3.28 sec
c) 9.7 sec
d) 1.33 sec
7. find the inverse of the function. (1 point)
f(x) = the cube root of quantity x divided by seven. - 9
a) f-1(x) = 21(x + 9)
b) f-1(x) = [7(x + 9)]3
c) f-1(x) = 7(x3 + 9)
d) f-1(x) = 7(x + 9)3
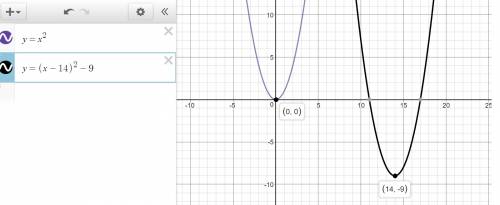
8. describe how the graph of y= x2 can be transformed to the graph of the given equation.
y = (x - 14)2 - 9 (1 point)
a) shift the graph of y = x2 right 14 units and then up 9 units.
b) shift the graph of y = x2 down 14 units and then left 9 units.
c) shift the graph of y = x2 right 14 units and then down 9 units
d) shift the graph of y = x2 left 14 units and then down 9 units
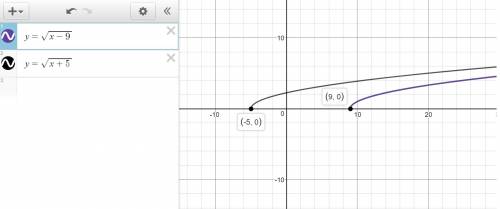
9. describe how to transform the graph of f into the graph of g.
f(x) = alt='square root of quantity x minus nine.' and g(x) = alt='square root of quantity x plus five. '
a) shift the graph of f right 14 units.
b) shift the graph of f right 4 units.
c) shift the graph of f left 14 units.
d) shift the graph of f left 4 units.
10. if the following is a polynomial function, then state its degree and leading coefficient. if it is not, then state this fact.
f(x) = -16x5 - 7x4 - 6 (1 point)
a) degree: -16; leading coefficient: 5
b) degree: 5; leading coefficient: -16
c) not a polynomial function.
d) degree: 9; leading coefficient: -16
11. write the quadratic function in vertex form.
y = x2 + 4x + 7 (1 point)
a) y = (x + 2)2+ 3
b) y = (x + 2)2 - 3
c) y = (x - 2)2 - 3
d) y = (x - 2)2 + 3
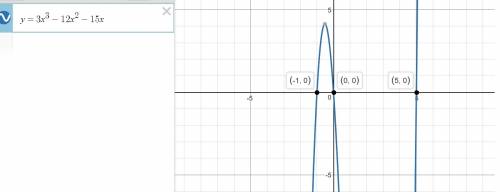
12. find the zeros of the function.
f(x) = 3x3 - 12x2 - 15x (1 point)
a) 0, 1, and -5
b) -1 and 5
c) 0, -1, and 5
d) 1 and -5
13. find a cubic function with the given zeros.
7, -3, 2 (1 point)
a) f(x) = x3 - 6x2 - 13x - 42
b) f(x) = x3 - 6x2 + 13x + 42
c) f(x) = x3 - 6x2 - 13x + 42
d) f(x) = x3 + 6x2 - 13x + 42
14. find the remainder when f(x) is divided by (x - k).
f(x) = 7x4 + 12x3 + 6x2 - 5x + 16; k = 3 (1 point)
a) 188
b) 946
c) 1,704
d) 2,512
15. use the rational zeros theorem to write a list of all potential rational zeros.
f(x) = x3 - 10x2 + 4x - 24 (1 point)
a) ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24
b) ±1, ±2, ±3, ±4, ±24
c) ±1, ± alt='one divided by two', ±2, ±3, ±4, ±6, ±8, ±12, ±24
d) ±1, ±2, ±3, ±4, ±6, ±12, ±24
need here asap, i would really appreciate the